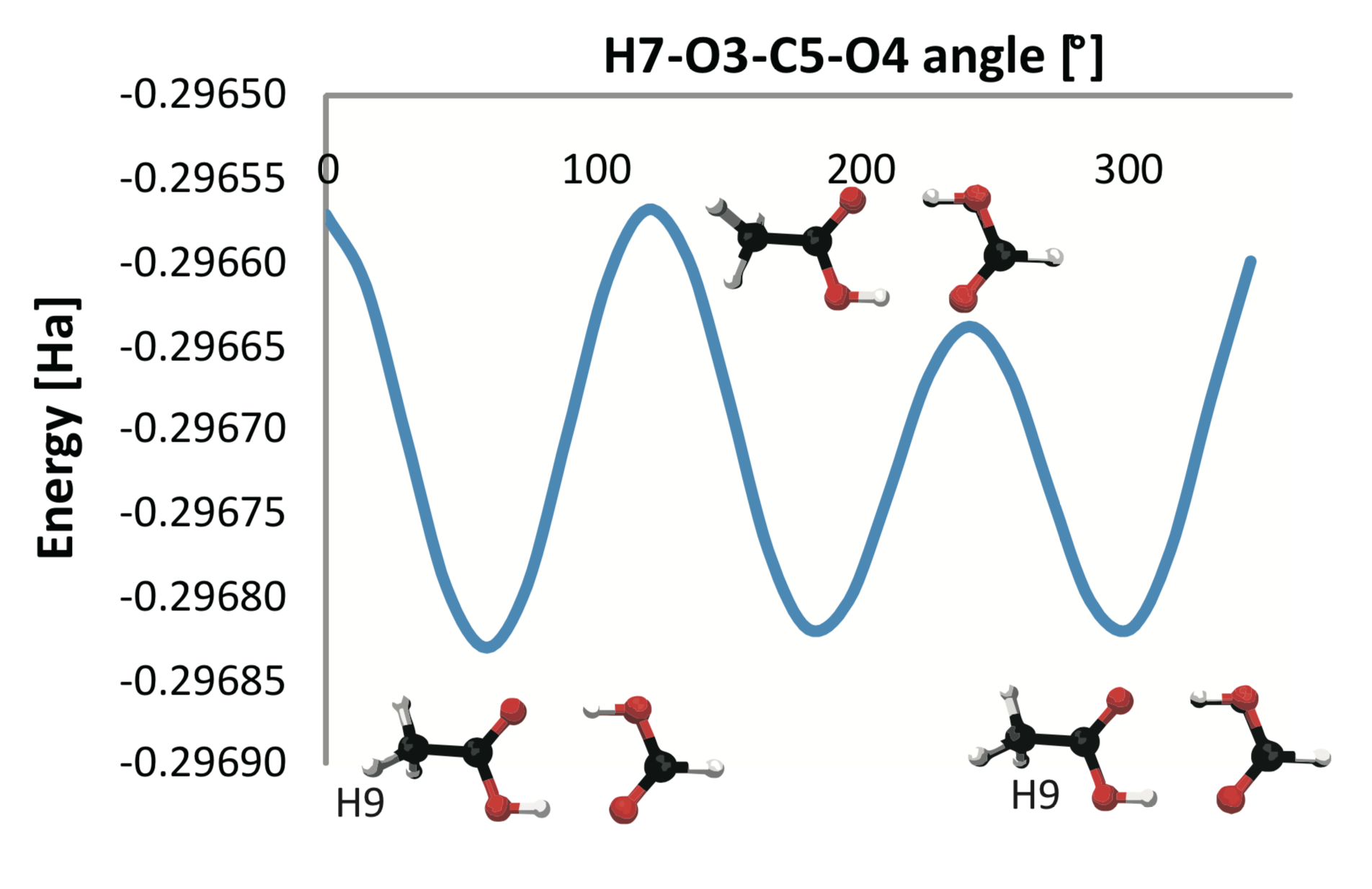
Fig. 1: Rotation of the methyl group of the molecule of dimer of formic and acetic acid produces a potential energy function. An appropriate approximation error for different functions depends on the analysis application. For example, when analyzing stable states (minima), the approximation error can be defined as the difference in number of minima.
A detailed study [1] how different approximations of functions given as samples at discrete locations influences the result of topological analysis.
Scalar functions account for a significant portion of the scientific data generated today carrying information about the behavior of a system, e.g., a molecule in a chemistry simulations. Topological analysis is an important tool in finding high level structure in these functions. Our study provides valuable information how different function approximations influence analysis results.
We study the influence of the definition of neighborhoods used for creating point connectivity on topological analysis of scalar functions.
We investigate two distances to measure the difference in topology: (i) the bottleneck distance for persistence diagrams and (ii) the distance between merge trees.
We investigated five types of neighborhoods and connectivity: (i) the Delaunay triangulation; (ii) the relative neighborhood graph; (iii) the Gabriel graph; (iv) the k-nearest-neighbor (KNN) neighborhood; and (v) the Vietoris–Rips complex.
We published a paper that discusses in detail how topological characterizations depend on the chosen connectivity and that provides recommendations on appropriate choices for neighborhood graphs.